Beyond Temporal Difference: A New Paradigm for Scalable Reinforcement Learning
Reinforcement Learning (RL) has long been dominated by a powerful but fundamentally limited technique: temporal difference (TD) learning. While foundational to many breakthroughs, TD learning faces significant challenges with scalability, especially in complex, long-horizon tasks where errors can compound catastrophically. What if there was a better way?
This post introduces a reinforcement learning algorithm built on an alternative paradigm: divide and conquer. By breaking down complex problems into smaller, manageable subproblems, this approach avoids the pitfalls of traditional methods. It does not rely on temporal difference learning and, as a result, scales gracefully to the kind of long-horizon challenges that are critical for the future of AI in robotics, dialogue systems, and beyond.
We will explore how this “divide and conquer” philosophy can be translated into a practical, powerful algorithm that outperforms established methods, offering a glimpse into a more scalable and robust future for reinforcement learning.
The Challenge of Learning from a Static World: Off-Policy RL
To understand the significance of this new approach, we first need to understand the environment in which it operates: off-policy reinforcement learning.
In the world of RL, algorithms are broadly divided into two classes: on-policy and off-policy.
On-policy RL requires a constant stream of fresh data. The learning agent can only use experiences collected by its current version. Every time the agent’s policy is updated, all previous data is discarded. Algorithms like PPO and its variants fall into this category. This is like a chef who can only learn from the dishes they cook right now, ignoring all their past culinary experiences.
Off-policy RL, on the other hand, is far more flexible. It allows the agent to learn from any data, regardless of its source. This can include old experiences from previous versions of the agent, datasets of human demonstrations, or vast repositories of information scraped from the internet. This makes off-policy RL more general, data-efficient, and powerful. It’s the method of choice in domains where collecting new data is expensive, time-consuming, or dangerous, such as robotics, healthcare, or complex dialogue systems.
While on-policy methods have seen significant progress and have developed scalable recipes for success, a truly scalable off-policy RL algorithm has remained elusive. The primary reason for this lies in the way current methods learn value.
The Twin Pillars of Value Learning and Their Cracks
In off-policy RL, the goal is typically to learn a “value function,” which estimates the long-term reward of being in a certain state or taking a certain action. The two dominant paradigms for learning this value are Temporal Difference (TD) learning and Monte Carlo (MC) evaluation.
The Instability of Temporal Difference (TD) Learning
TD learning, most famously represented by Q-learning, is the workhorse of modern RL. It works by “bootstrapping”—updating its current value estimate based on other, future value estimates. The update rule, known as the Bellman update, looks like this:
$Q(s, a) \gets r + \gamma \max_{a’} Q(s’, a’)$
In simple terms, the value of the current state-action pair Q(s, a) is updated using the immediate reward r plus the discounted γ maximum value of the next state Q(s', a').
The problem is that this process is like a game of telephone. Any small error in the value estimate for the next state Q(s', a') is propagated back to the current state Q(s, a). In tasks with long horizons, this update happens thousands of times, and these small errors accumulate, snowballing into a massive, destabilizing error that renders the value function useless. This fundamental issue is what prevents TD learning from reliably scaling to very long tasks.
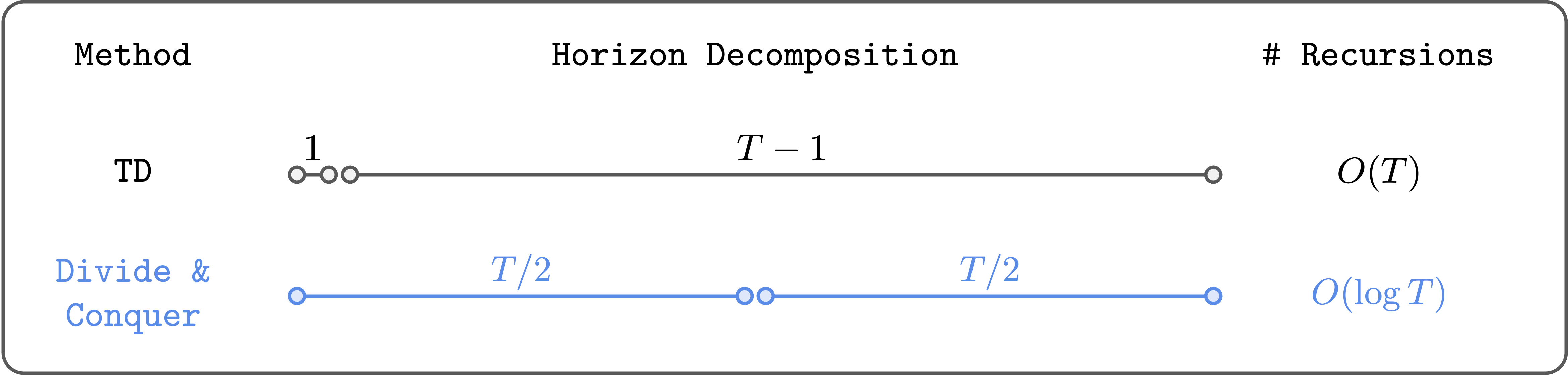
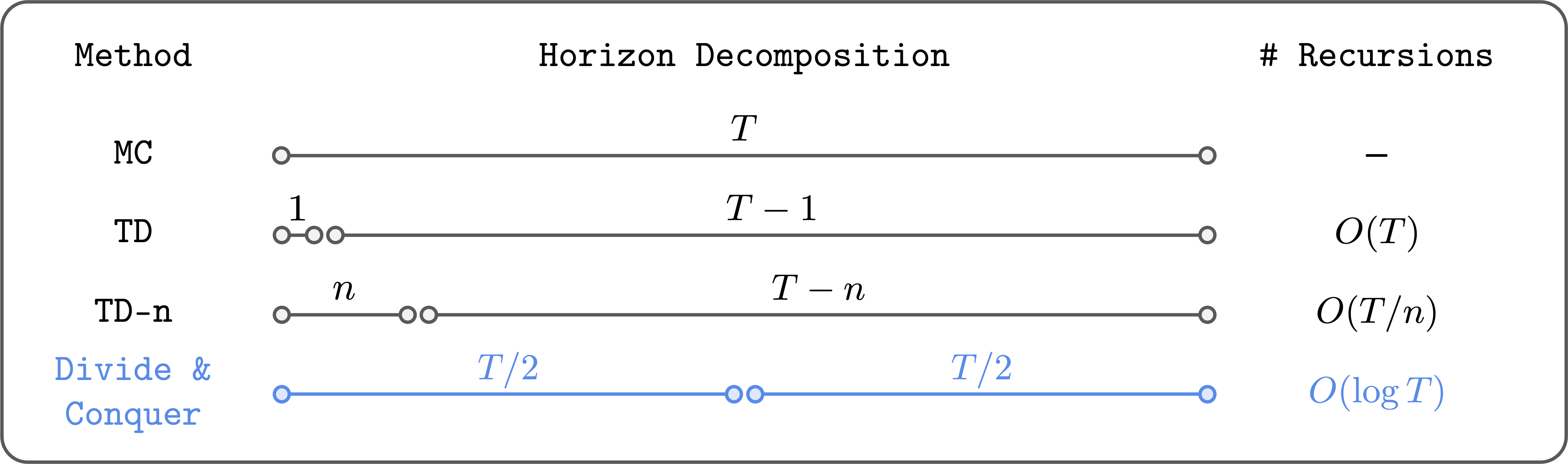
The Compromise: n-step TD Learning
To combat this error accumulation, practitioners often mix TD learning with Monte Carlo (MC) returns, which use the full sequence of actual rewards from experience. This hybrid is known as n-step TD learning (TD-n).
The TD-n update rule is:
$Q(s_t, a_t) \gets \sum_{i=0}^{n-1} \gamma^i r_{t+i} + \gamma^n \max_{a’} Q(s_{t+n}, a’)$
Here, the algorithm uses the real, observed rewards for the first n steps and only then bootstraps from the value function Q(s_{t+n}, a'). This reduces the number of recursive Bellman updates by a factor of n, which helps mitigate error accumulation.
However, this is a deeply unsatisfactory solution.
- It’s a Band-Aid, Not a Cure: It doesn’t solve the fundamental problem; it just reduces the number of error-propagating steps by a constant factor. For truly long-horizon tasks, the problem remains.
- It Introduces New Problems: As the step-size
nincreases, the variance of the updates grows, and the policy can become suboptimal. - It Requires Tedious Tuning: The optimal value of
nis task-dependent and must be carefully tuned, adding another layer of complexity to the experimental process.
This begs the question: is there a fundamentally different way to approach value learning that sidesteps these issues entirely?
A Third Path: The Power of Divide and Conquer
We propose that a third paradigm, divide and conquer, offers a more elegant and scalable solution to off-policy RL. This principle is foundational in computer science, powering classic, highly efficient algorithms like quicksort and the Fast Fourier Transform. Instead of chipping away at a problem one step at a time, divide and conquer breaks it into smaller, independent subproblems, solves them, and combines their solutions.
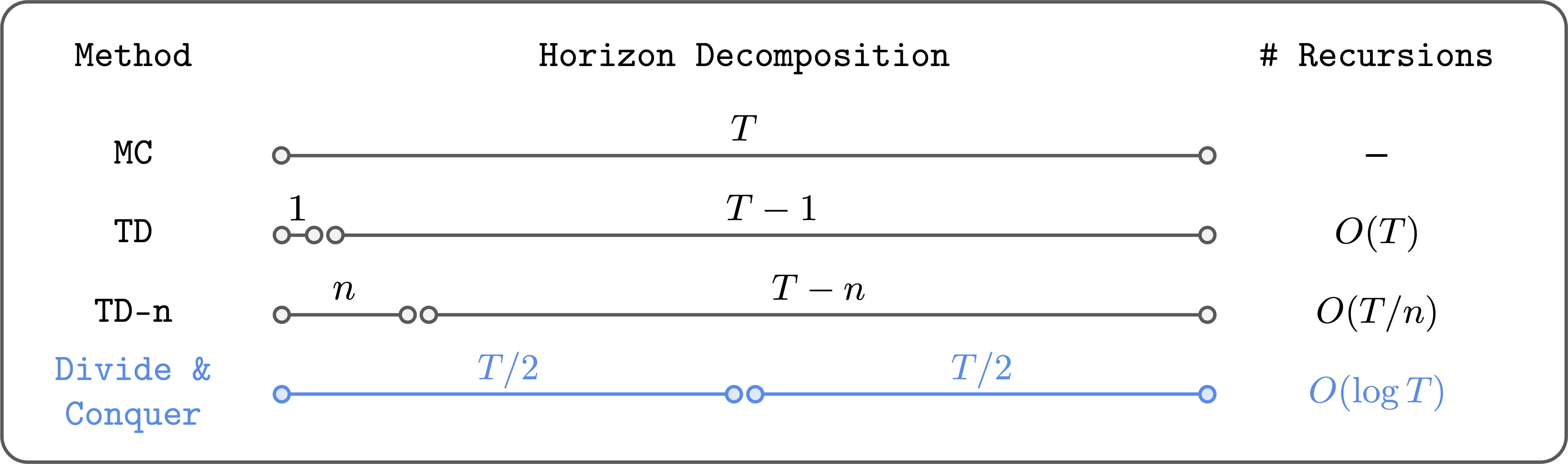
In the context of RL, this means dividing a long trajectory into two equal-length segments, calculating their values, and then combining them to get the value of the full trajectory. This recursive process has a profound implication: it can reduce the number of Bellman-like recursions logarithmically, not linearly.
For a 1,000-step task, a standard TD approach might perform 999 recursive updates. A 10-step TD approach would perform 99. But a divide-and-conquer approach would require only about 10 levels of recursion (since 2¹⁰ ≈ 1000). This logarithmic scaling is exponentially more efficient and robust against error accumulation.
The conceptual advantages are clear:
- Logarithmic Scaling: Drastically reduces the depth of value propagation, minimizing error accumulation.
- No Hyperparameter
n: It naturally adapts to any horizon length without requiring manual tuning of a step size. - Maintains Optimality: It doesn’t suffer from the high variance or suboptimality issues associated with large
nin TD learning.
The idea itself is not new, but a practical, scalable implementation has remained out of reach. Until now.
From Theory to Practice: Introducing Transitive RL (TRL)
Our recent work, developed with Aditya, introduces a practical algorithm that successfully scales this divide-and-conquer concept to complex domains. We achieve this within the framework of goal-conditioned RL, a subfield where the agent learns a versatile policy to reach any achievable state (goal) from any other state. This setup provides the perfect structure for a divide-and-conquer approach.
The core insight comes from the triangle inequality. In a deterministic environment, the shortest path distance between a starting state s and a goal g, denoted d*(s, g), obeys the following rule for any intermediate waypoint w:
$d^(s, g) \leq d^(s, w) + d^*(w, g)$
We can translate this geometric principle into a “transitive” Bellman update rule for our value function V(s, g), which represents the discounted reward for reaching g from s.
$V(s, g) \gets \max_{w \in \mathcal{S}} V(s, w)V(w, g)$
Intuitively, this means the value of traveling from s to g can be found by identifying the optimal midpoint w and combining the values of the two sub-journeys: s to w and w to g. This is the divide-and-conquer update we were searching for!
The Practical Hurdle and Our Solution
There’s a critical challenge here: how do we find the optimal midpoint w? In a simple, tabular world, we could iterate through every possible state. But in the vast, continuous state spaces of modern RL problems, this is computationally impossible. This single issue has stalled progress on this idea for decades.
Our work, which we call Transitive RL (TRL), introduces a practical solution to this problem:
Constrain the Search: Instead of searching over the entire infinite state space for the optimal
w, we restrict the search to only those states that appear in the offline dataset, specifically those that lie on the trajectory between the startsand goalg. This dramatically narrows the search space to a manageable set of plausible candidates.Soften the
maxOperator: Themaxoperator is known to cause value overestimation. Instead of performing a hard search for the single bestw, we use a “soft” version by framing the problem as an expectile regression task. This allows the network to learn an optimal combination of subgoals in a more stable and efficient manner.
The final loss function we minimize is:
$\mathbb{E}[\ell^2_\kappa (V(s_i, s_j) - \bar{V}(s_i, s_k) \bar{V}(s_k, s_j))]$
where (s_i, s_k, s_j) are points on a trajectory such that i ≤ k ≤ j, V is the value network, V-bar is the target network, and l² is the expectile loss. This elegant formulation avoids a costly search and prevents value overestimation, making divide-and-conquer value learning finally practical.
Putting TRL to the Test: Performance on Ultra-Long-Horizon Tasks
To validate TRL, we tested it on some of the most difficult tasks from OGBench, a benchmark designed for offline goal-conditioned RL. We focused on the humanoidmaze and puzzle environments, which require an agent to perform combinatorially complex skills over horizons of up to 3,000 environment steps. These are precisely the kinds of long-horizon tasks where traditional TD learning fails.
Here is a glimpse of TRL in action:
The quantitative results are equally compelling. We compared TRL against a suite of strong baselines, including methods based on TD learning, Monte Carlo returns, and quasimetric learning.
| Environment | Task | TRL (Ours) | TD-n (Best) | TD-1 (Q-Learning) | MC (Pure) | Other SOTA |
|---|---|---|---|---|---|---|
| humanoidmaze | large-v2 | 1.00 ± 0.00 | 0.99 ± 0.01 | 0.00 ± 0.00 | 0.93 ± 0.04 | 0.81 ± 0.02 |
| puzzle | large-v1 | 0.28 ± 0.02 | 0.28 ± 0.03 | 0.02 ± 0.01 | 0.23 ± 0.02 | 0.22 ± 0.02 |
| puzzle | large-v2 | 0.30 ± 0.02 | 0.29 ± 0.02 | 0.00 ± 0.00 | 0.28 ± 0.02 | 0.22 ± 0.03 |
As shown in the table, TRL achieves state-of-the-art performance, significantly outperforming standard TD learning and matching or exceeding other highly tuned methods.
Perhaps the most revealing result comes from a direct comparison with n-step TD learning across various values of n.
This plot perfectly illustrates the power of the divide-and-conquer paradigm. For each task, there exists an optimal n for TD-n that performs very well, but this optimal n is different for each task and must be found through extensive tuning. TRL matches the performance of the best-tuned TD-n on all tasks, without needing to set n at all. It automatically adapts to the problem’s horizon by recursively splitting it, delivering the benefits of long-horizon value propagation without the associated costs of tuning and instability.
The Road Ahead: The Future of Divide-and-Conquer RL
Transitive RL represents a promising first step, but this is just the beginning of a longer journey. Several exciting research directions and open questions remain.
Generalizing Beyond Goals: The most critical next step is to extend TRL from goal-conditioned RL to the broader setting of general, reward-based RL. While it is theoretically possible to frame any RL problem as a goal-conditioned one, developing a direct and practical divide-and-conquer structure for arbitrary reward functions is a major open challenge.
Embracing Stochasticity: The current version of TRL assumes deterministic dynamics. However, many real-world environments are stochastic, either due to inherent randomness or partial observability. Extending the transitive value updates to handle uncertainty, perhaps through insights from stochastic triangle inequalities, will be crucial for real-world deployment.
Refining the Algorithm: There is ample room to improve TRL itself. Future work can explore more sophisticated methods for selecting subgoal candidates, further reduce the need for hyperparameter tuning, and improve training stability to make the algorithm even more robust and user-friendly.
I remain convinced that finding a truly scalable off-policy RL algorithm is one of the most important unsolved problems in machine learning. The final solution may come from model-based RL, a breakthrough in TD learning, or, as I believe, from the paradigm of recursive decision-making. The success of divide-and-conquer strategies in other areas of AI, from log-linear attention to recursive language models, suggests a powerful underlying principle at play. TRL demonstrates that this principle can unlock new capabilities in reinforcement learning, and I am incredibly excited to see what comes next.






Comments