Decoding word2vec: A New Theory Reveals How It Truly Learns
The world of artificial intelligence is built upon layers of foundational discoveries, and few are as influential as word2vec. Developed over a decade ago, this algorithm revolutionized natural language processing (NLP) by learning dense vector representations of words, known as embeddings. These embeddings capture complex semantic relationships, allowing models to understand language in a way that was previously unimaginable. Yet, despite its widespread use and its role as a precursor to modern large language models (LLMs), a deep, quantitative understanding of how word2vec learns has remained elusive. For years, we’ve observed its remarkable capabilities without a complete, predictive theory to explain the process.
That is, until now. A new paper finally provides a comprehensive theoretical framework that demystifies the learning dynamics of word2vec. The research proves that under realistic and practical conditions, the intricate process of learning word embeddings simplifies to a well-understood mathematical operation: unweighted least-squares matrix factorization. This breakthrough allows us to solve the gradient flow dynamics in closed form, revealing that the final, learned representations are elegantly determined by Principal Component Analysis (PCA). This insight not only answers long-standing questions about word2vec but also provides a critical stepping stone for understanding feature learning in the more complex language models of today.

The Enduring Mystery of word2vec
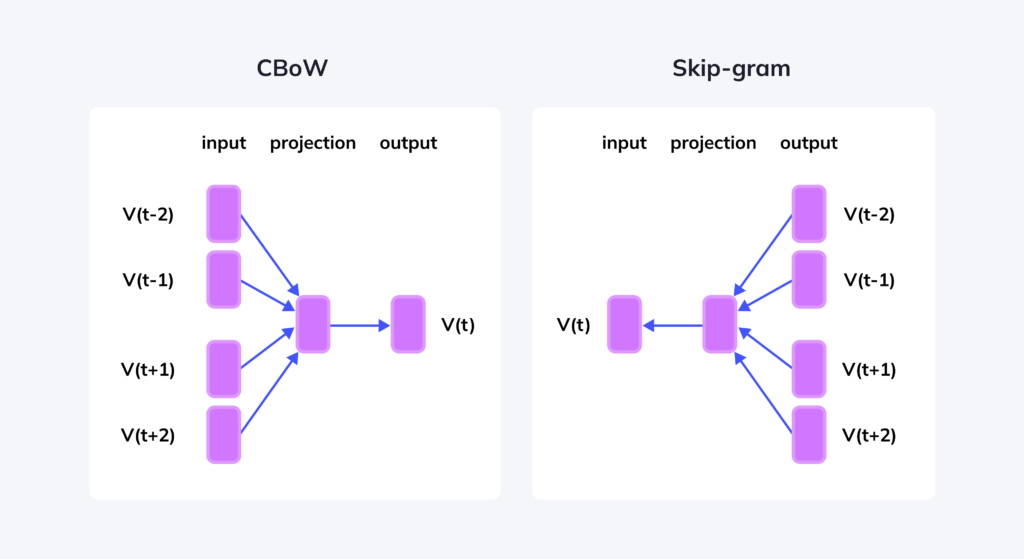
Before diving into the specifics of this new theory, it’s essential to appreciate the problem word2vec was designed to solve and the fascinating properties it exhibits. At its core, word2vec is a simple, two-layer linear network trained via self-supervised gradient descent on a massive text corpus. It learns by predicting a word based on its context (the Skip-gram model) or predicting a context based on a word (the Continuous Bag-of-Words model).
The outcome of this training is a high-dimensional vector space where each word is represented by a unique vector, or embedding. The magic lies in the geometry of this space. Words with similar meanings are located close to one another. More impressively, the relationships between words are encoded as consistent vector offsets. This is the foundation of the famous “word analogy” task, where word2vec can solve “man is to woman as king is to ?” by performing simple vector arithmetic: vector('king') - vector('man') + vector('woman'), which results in a vector very close to vector('queen').
This phenomenon is a manifestation of the linear representation hypothesis, which posits that meaningful concepts can be represented as linear directions or subspaces within the embedding space. This hypothesis has gained significant traction recently, as similar structures have been discovered within the internal representations of massive LLMs. This property is not just an academic curiosity; it enables powerful techniques for inspecting the internal states of models and even steering their behavior in desired directions.
Given that word2vec is essentially a minimal neural language model, understanding precisely how it learns these structured linear representations is a fundamental prerequisite for dissecting the more opaque workings of its larger, more complex successors.
A Breakthrough in Understanding: Learning as Matrix Factorization
The central finding of the new research is a powerful simplification of the learning process. The authors demonstrate that if the model’s embedding vectors are initialized with very small random values, effectively starting near the origin, the learning dynamics unfold in a predictable and structured manner. Under a few mild and practical approximations, the entire contrastive learning problem elegantly reduces to unweighted least-squares matrix factorization.
This is a significant theoretical leap. Instead of a complex, non-convex optimization problem that is difficult to analyze, the learning process becomes equivalent to finding the best low-rank approximation of a specific target matrix. This reframing allows the researchers to solve the learning dynamics completely and analytically. The conclusion is striking: the features word2vec learns are not arbitrary but are precisely the principal components of this target matrix. In other words, word2vec is, for all intents and purposes, performing PCA.
The Step-by-Step Learning Process: One Concept at a Time
This theoretical framework reveals that word2vec does not learn everything at once. Instead, it acquires knowledge in a sequence of discrete, well-defined steps. When training begins with near-zero embeddings, the model collectively learns one “concept”—an orthogonal linear subspace—at a time.
Imagine diving into a new, complex field like advanced mathematics. Initially, all the terminology is a confusing jumble. Words like “function,” “functional,” “operator,” and “matrix” might seem interchangeable. However, with repeated exposure to different examples and contexts, these terms begin to separate in your mind. You start to grasp the distinct meaning of each one, and they organize themselves into a coherent conceptual framework.
The learning process in word2vec mirrors this human experience.
At each discrete learning step, the model identifies and learns a new, dominant concept present in the data. This effectively increments the rank of the embedding matrix, giving each word vector an additional dimension to express its meaning more precisely. The embedding space expands, one orthogonal direction at a time, until the model’s capacity is fully utilized.
A crucial aspect of this process is that once these linear subspaces are learned, they do not rotate or change. They become fixed features of the model. This theory doesn’t just describe this process; it allows us to compute these features ahead of time, in closed form. They are simply the eigenvectors of a target matrix defined entirely by the statistical properties of the training corpus and the model’s hyperparameters.
The Formula for Knowledge: What Features Does word2vec Actually Learn?
So, what are these features that word2vec learns sequentially? The answer is remarkably direct. The latent features correspond to the top eigenvectors of a specific target matrix, which we can call $M^{\star}$. This matrix is defined as follows:
\[M^{\star}_{ij} = \frac{P(i,j) - P(i)P(j)}{\frac{1}{2}(P(i,j) + P(i)P(j))}\]
Let’s break down this formula into its components:
- $i$ and $j$: These represent two different words in the vocabulary.
- $P(i,j)$: This is the co-occurrence probability, or the likelihood that words $i$ and $j$ appear together within a certain context window in the text corpus.
- $P(i)$: This is the unigram probability, which is simply the frequency of word $i$ appearing in the corpus. The term $P(i)P(j)$ represents the probability that the two words would appear together by pure chance if their occurrences were independent.
The numerator, $P(i,j) - P(i)P(j)$, is a measure of how much more (or less) often two words appear together than expected by chance. This is closely related to Pointwise Mutual Information (PMI), a common measure in information theory. The denominator acts as a normalization term.
The profound takeaway is this: the entire training process of word2vec, under these conditions, is equivalent to running PCA on this matrix $M^{\star}$. The model sequentially finds the optimal low-rank approximations of this matrix.
When this theory is applied to real-world data, such as a large Wikipedia corpus, the learned features are not only mathematically defined but also humanly interpretable. For instance:
- The top eigenvector (the first and most dominant feature learned) corresponds to words associated with celebrity biographies.
- The second eigenvector captures a concept related to government and municipal administration.
- The third eigenvector relates to geographical and cartographical terms.
Each subsequent eigenvector represents another distinct, topic-level concept embedded within the statistical fabric of the language.
Theory Meets Reality: Visualizing the Learning Dynamics
Theoretical claims are most powerful when backed by empirical evidence. The predictions made by this new framework align exceptionally well with what is observed in actual word2vec training.

The charts above illustrate this remarkable agreement. The plot on the left demonstrates that the model learns in a series of distinct steps. With each step, the effective rank of the embedding matrix increases by one, leading to a stepwise decrease in the training loss. This is not a smooth, continuous descent but a quantized, structured progression.
The diagrams on the right offer a glimpse into the latent embedding space at three different points in time. They visually confirm the theory: the cloud of embedding vectors first expands along one direction, then a second orthogonal direction, and then a third. By examining the words that align most strongly with each new direction, we can see that each step corresponds to the discovery of an interpretable, topic-level concept. The match between the closed-form theoretical solution and the numerical experiment is nearly perfect.
The Fine Print: Conditions and Approximations
Of course, this elegant simplification relies on a few “mild approximations.” It is important to understand these conditions to appreciate the scope of the result. The theory holds under the following assumptions:
- Quartic approximation: The objective function is approximated by its fourth-order Taylor expansion around the origin.
- Hyperparameter constraint: A specific constraint is placed on the algorithmic hyperparameters, which is consistent with practical settings.
- Small initialization: The initial embedding weights are set to be very small, close to zero.
- Small learning rate: The gradient descent steps are assumed to be vanishingly small (infinitesimal).
Fortunately, these conditions are not overly restrictive. In fact, they closely mirror the setup described in the original word2vec paper. A crucial strength of this theory is that it makes no assumptions about the data distribution itself. This distribution-agnostic nature is rare and powerful, as it means the theory can predict exactly which features will be learned based solely on measurable corpus statistics and chosen hyperparameters. This provides a level of predictive power that is seldom achieved in theories of machine learning.
Putting the Theory to the Test: Performance and Practical Insights
To validate that these approximations do not lead to a significant departure from the original algorithm’s behavior, we can compare their performance on standard benchmarks. The analogy completion task serves as a coarse but effective indicator.
| Model | Analogy Completion Accuracy |
|---|---|
Original word2vec | 68% |
| Approximate Model (Theory) | 66% |
| PPMI (Classical Alternative) | 51% |
As the table shows, the approximate model studied in the theory achieves an accuracy of 66%, which is remarkably close to the 68% achieved by the true word2vec implementation. Both significantly outperform the classical alternative method based on PPMI, which only reaches 51%. This confirms that the theoretical model provides a faithful and accurate description of word2vec’s practical performance.
Beyond validating the overall process, the theory also provides a powerful lens for studying more nuanced phenomena. For example, the researchers applied it to understand the emergence of abstract linear representations, such as binary concepts like masculine/feminine or past/future tense. They found that word2vec constructs these representations through a series of noisy learning steps. The geometry of these representations is well-described by a spiked random matrix model.
This analysis reveals a fascinating trade-off:
Early in training, the semantic signal in the data is strong and dominates the learning process, leading to the formation of clear, abstract concepts. However, as training progresses and the model learns finer-grained features, noise can begin to dominate, potentially degrading the model’s ability to resolve these high-level linear representations cleanly.
Conclusion: A Foundation for Understanding Modern AI
This work provides one of the first complete, closed-form theories of feature learning for a minimal yet highly relevant natural language processing task. By demonstrating that word2vec effectively performs a sequential PCA on a specific statistical matrix, it replaces a long-standing mystery with a clear and predictive mathematical framework.
This achievement is more than just an academic exercise in understanding a decade-old algorithm. It represents a crucial step forward in the broader scientific endeavor to develop realistic, analytical solutions that describe the performance of practical machine learning systems. As we continue to build larger and more powerful models, a solid theoretical understanding of their foundational predecessors is indispensable. By decoding word2vec, we gain invaluable insights that light the way toward a deeper understanding of the incredible, emergent capabilities of modern artificial intelligence.
To explore the full mathematical details and proofs, you can read the complete paper: Link to full paper







Comments